How is math used in dance
Dancing: Revealing the Beauty of Mathematics
Posted on by admin
Post Views: 32,598
‘Mathematics is an easy and exciting subject to learn‘. When you hear or read this statement, what is on your mind, will you agree or disagree?. Mathematics is embedded in our daily lives, our culture, in which art is a part of. In painting, the role of mathematics has already been widely applied. For example in one the most famous paintings, The Mona Lisa, ratio plays an important role. In another kinds of art, namely dance, mathematics also has an important role.
To some, Mathematics is generally seen as a bunch of numbers and formulas, which is considered to be near polar opposites of dancing. General society might see that these two worlds have nothing in common. Yet, when we look closely, similarities and connections reveal themselves.
There are thousands of cultures spread around the globe and each have their own dances with various kinds of moves. As we looked closely into these dances, we can see that they are made of rhythm, shapes, and patterns. These can be linked to the mathematical concepts. Therefore, mathematics can be taught using dance. Teaching mathematics with dancing can help students to understand abstract concepts of mathematics more joyfully. Implementing mathematics in ‘real life’ such as in dancing will certainly help to erase the stigma of the subject being dry and inaccessible.
Expert in mathematics from Australia, Dr. Mathews says “Math involves creating symbols and putting them together to represent the real world”. Based on this theory, students become the mathematics themselves. It has been proven in an Australian based school that students understand the mathematical concept better when they are encourage to be creative and create their own symbol, relating them with stories in their own world.
Mathematical concepts such as Geometry can be introduced to students by teaching them dancing. This concept can be seen in the positioning of a dancer’s body in relation to themselves and their surroundings. Within the dancer’s body, he or she can create shapes, angles, and lines which contributes to the effect of the dance. Concerning shapes and angles, dancers need to focus on the angles they make with their bodies to form the correct shapes. Meanwhile, talking about the lines concept through the dance, dancers often have to think about staying parallel to other dancers to preserve formations. They need to keep the same distance between each other no matter how they move.
Picture of math teachers dance performance
Furthermore, Geometry is also used to unify between one and another dancer. Without Geometry, dancers would not be able to be synchronized and create shapes. Besides Geometry, everything in dancing has to do with patterns. Dancers memorize patterns in the steps in their dances.
The rythm in music usually consist of patterns in the form of beats. This pattern is generally syncronized with the dancers’ movement.
One of a well-known dance which employs the used of Geometry is Saman. This dance is originated from Aceh, Indonesia. The Saman dance requires high movement synchronization among each dancers, the timing of each dancer plays an important role. From this dance we can also explore other mathematics concepts such as line, symmetry, and patterns. The larger number of dancer, the more possible relations of lines, shapes and patterns arise from their interacting bodies.
Another example of mathematics used in dancing is in figure skating. Assistant Professor of mathematics at Towson University states “Figure skating is a great model for mathematical instruction”. Brian Shackel and Marion Alexander of the University of Manitoba mentioned that the angles of the skaters, is an important aspect in ice skating such as when they jump, spin, skid, glide, and even during landing.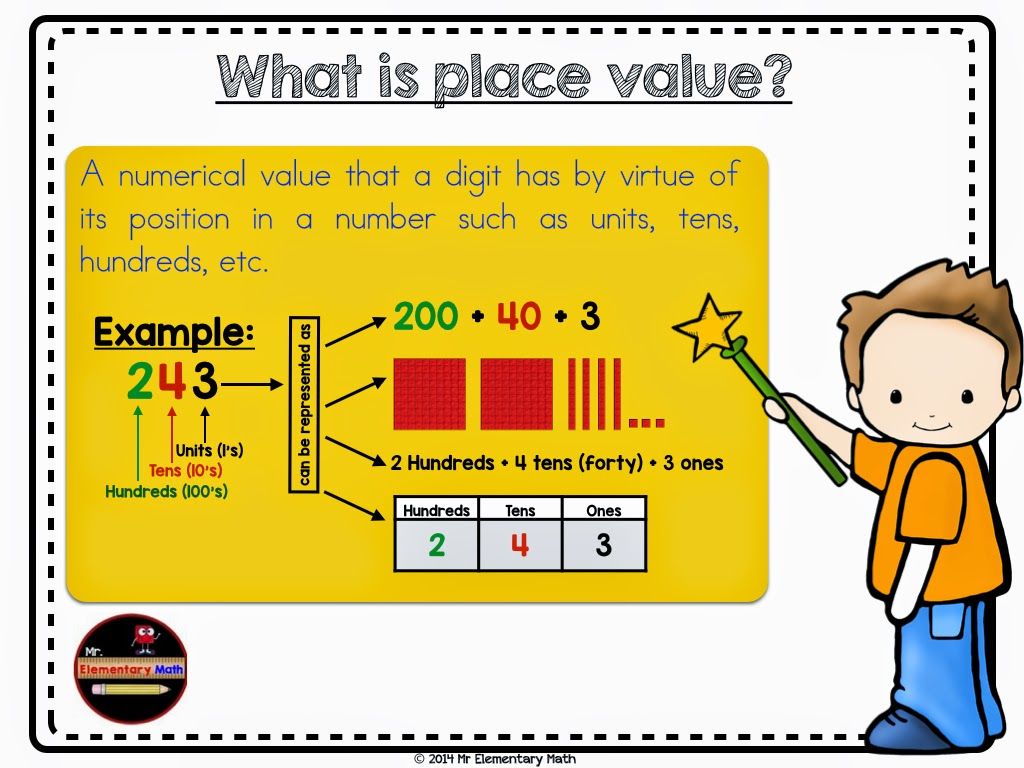
The more accurate the angles used in each stage, the higher the score they will get.
Picture of SEAQiM event “Understanding SEAMEO Countries Culture”
With this in mind, SEAQiM incorporated the idea of mathematics as an art in the session Understanding SEAMEO Countries Culture. Having backgrounds in mathematics, teachers are able to present a great dancing performance in a very limited amount of time. The dance consists of symbols and patterns as well as timing of the rhythm, which are basically mathematical concepts performed in reality.
For people out there who think dance has nothing to do with mathematics, think twice. Mathematics is not merely just equation to be memorized. How to turn this subject into a fun activity, goes back to the teacher’s creativity. One way to teach this subject is through dancing.
Pada tahun 2021 ini, pastinya kalian bingung dalam memilih situs slot online terbaik yang ada di Indonesia. Banyak sekali bermunculan website tidak jelas dan tidak memberikan keuntungan bagi para member serta tidak mempunyai izin resmi
Share this article
Posted in Math Articles.
Mathematics in Dance |
Dance in Primary school encourages flexibility in thinking, creativity, and perseverance. These are all necessary for building skills for mathematics.
There is a history of Mathematics and Arts as far back as the ancient Greeks. Along with the Egyptians, they used the Golden ratio to build many of their monuments. Leonardo da Vinci incorporated mathematics as an important part of his art works.
How do dancers use Mathematics?
Different dance styles use Mathematics in different ways. For example, Latin dancers express rhythm as fractions when they talk about whole, half and quarter beats. Ballet dancers observe the angle of the body, legs, and arms in positions such as holding a leg in the air at a 90 degree angle.
In dance we talk about our feet being in parallel and moving on diagonals. We phrase our music in counts of 8, 16 or 32.
Traditionally, in ballet, the stage is divided into quarters and eighth to position the dancers correctly for unison and for the stage lighting plan.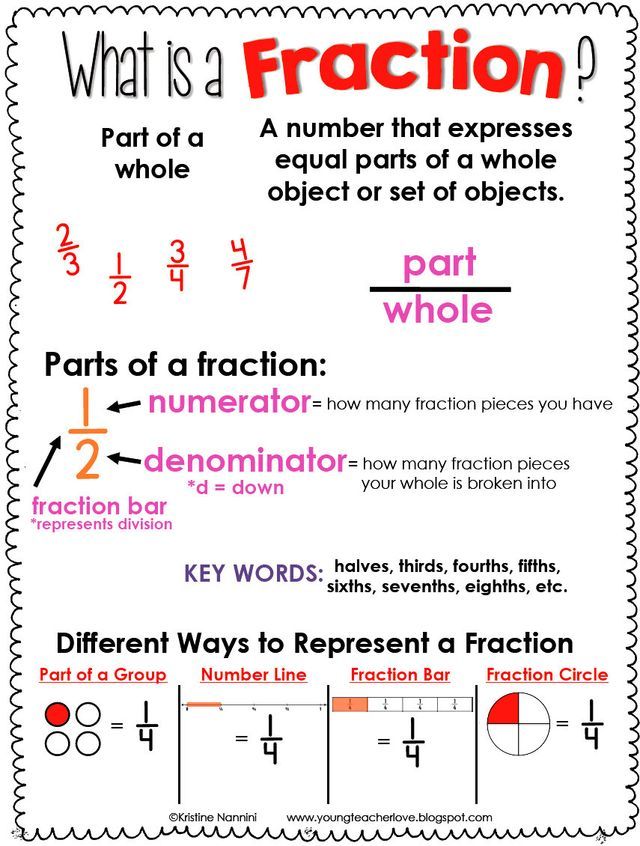
The dance works themselves are even in two halves or three thirds.
More impressively, the dancer calculates distance between other dancers and objects throughout their performances. They even adjust these distances in response to the different size or shape of the space they perform in.
Having a heightened state of spatial awareness, ability to manipulation of space and time and proprioceptive self-imaging is a part of learning the craft of dance.
Dancers are skilled at looking for patterns in choreography and use these patterns to remember movement.
Creating a Mathematics and Dance lesson
Educationalists like Dewey, Montessori and Whitehead have identified movement as an effective way to promote learning (Evangelopoulou, 2014). Thurston (1994) believed that people were able to think on a larger scale when using spatial imagery. This was later supported by the work of Watson (2005) who investigated the ‘use of kinaesthetic experiences associated with dance.
Watson explored using dance teaching to promote engagement and learning in spatial, rhythmic, structural and symbolic aspects of mathematics’(Evangelopoulou, 2014).
The research of the late Professor Tom Cooper (Queensland University of Technology) and Dr Christopher Mathews (Griffith University) highlights that Maths and Dance is a way of bringing together the abstract and the tangible within a framework of children’s lived experiences. YuMi Deadly Maths is based on their findings and shows how the theory of bringing these two ways of learning together can work in the Primary classroom.
Starting out
Before designing your Dance and Mathematics activity it is important to watch this video to understand the phases that the lesson needs to cover to be most effective.
Erik Stern and Karl Schaffer, authors of Math Dance and founders of Dr Schaffer and Mr Stern Dance Ensemble, believe “choreographic and mathematic thinking are composed of similar building blocks”.
They involve similar processes like noting changes, remembering sequences, asking if things are bigger or smaller, checking your work to see if its consistent and much more (Stern & Scaffer, 2019 TED Talk).
How can we learn about Maths in a Primary dance class?
There are some obvious processes that lend themselves for using Maths in your dance class.
Look for a pattern.Have children identify patterns that may occur in a piece of choreography. This may be something they have learned themselves or it could be a professional piece of choreography they observe.
The pattern could be in the floor pattern (where the dancers move in the space) or in the dynamics (how the dancers move in the space) of the dance work.
Identify the pattern and represent each section with a different symbol. This teaches them about choreographic forms (eg. binary, ternary form) and about taking an abstract symbol to represent a concrete idea.
The children approximate how far each movement travels across the floor and then draw a model of their dance including the actual measurements of each movement.
Reduce the size of the space and repeat the process.
They then create a table that answers the following questions. What is the difference between the movements in the first model and the movements in the second? How did you have to change the movements to adapt it to the second version?
Ensure that a part of the table allows them to show their working.
These movement activities require advanced thinking skills in both mathematics and dance.
Try to use Polya’s Problem Solving Model when doing these kinds of activities by dividing the lesson into Think, Plan, Do and Lookback activities. It fits nicely with a creative Arts approach and encourages children to see further synergies in the processes used for problem solving in Dance and Mathematics.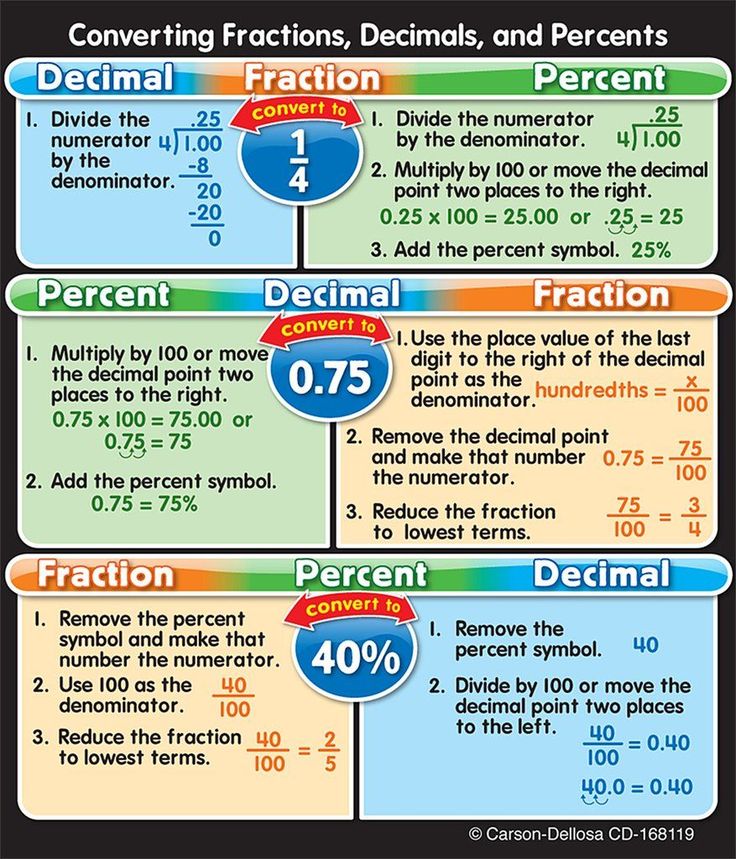
Themes and ideas for teaching Mathematics Dance
The obvious themes that link Mathematics to Dance are about shapes, patterns, angles, symmetry, geometry, multiplication, subtraction, division, and addition. However, by looking at the dancers’ bodies in relation to one another, and the space in which the dancer moves, we can design activities that require more complex consideration.
Patterns of beats and rhythmic changes in the music or the way the body moves and responds to the music can also be a starting point for ideas.
Shape transformation that investigates reflection, rotation and translation are also great for dance activities.
Look at the statistical properties of a piece of dance. How many jumping movements were there versus balancing ones? Sharp versus sustained? Suspended versus falling?
Social dances are wonderful ways to investigate Maths as they are about symmetry, changing patterns and are easy for children to illustrate from an overhead view.
The Maypole dance offers many challenges for the Maths students as you can look at the size of the pole, the angle of the ribbons (, the distance between the dancers and the maypole and the percentage that it diminishes through the course of the dance.
For an older age group, you could design an activity where they predict how many geometric patterns using 6 people with different coloured ribbon combinations are created. But perhaps we are now looking at proofs!
You can see how exciting Mathematics and Dance can be.
Using dance to teach about mathematics and mathematics to enhance learning about dance can result in positive learning experiences for Primary students.
Using dance in your Maths classroom can lead to a better understanding of mathematical concepts, increase motivation, and encouraged creativity and critical thinking. It acts to acknowledge the part number and logic plays in the art of Dance in a professional environment and makes students see the real-world applications of Maths learning in a creative context.
For more ideas about how to integrate Dance in your Maths class see Dance and Maths: Angles and the free lesson plan Coding for Kids.
References
Evangelopoulou, Polyxeni (2014). The impact of integrating dance and movement in maths teaching and learning in preschool and primary school settings. Masters research (International and Comparative Education). Stockholm University.
Thurston, W. P. (1994). On proof and progress in mathematics. Bulletin of the American Mathematical Society, 30 (2), 161-177.
Watson, A. (2005). Dance and Mathematics: Engaging Senses in Learning. Australian Senior Mathematics Journal, 19 (1), 16-23.
Project on the topic "Mathematics in dance"
Municipal budgetary Educational Institution
"Gymnasium No. 4"
Project
Pupils of class 9 B
Bondarenko Alexandra Vitalievna
Project manager:
Mathematics teacher
Androsova Elena Anatolyevna
Kursk
Cuties
Introduction
1.
Geometry in dance 1.1 Warm-up
1.2 Stretching
1.3 Figure
1.3.1 Diagonal
1.3.2 Circle
1.3.3 Symmetry
1.3.4 Asymmetry
1.3.5 Relationship between symmetry and asymmetry
1.4 Equilibrium and balance
Chapter 2. Algebra in dance
2.1 Dance and functions
2.2 Rhythm
2.3 Dance of the Planets
Chapter 3. Practice
3.1 Task
Conclusion
Sources
Introduction
Where there is beauty, there are laws mathematics .
(G. H. Hardy)
each a student at school is engaged in mathematics, and only a few are fond of dancing. So how this occupation has been my hobby for 10 years, and I I do to this day, it became interesting to me whether there is between these two concepts of connection, and how it manifests itself.
Relevance project topics : exact tasks develop thinking, logic, a complex of analytical skills, discover patterns, determine connections among phenomena. It has also been proven that dancing has a beneficial effect not only on physical form, but also on mental abilities, spatial imagination. Therefore, a reasonable combination of dancing and mathematics gives opportunity to improve the mind.
Purpose : find common ground between dance and mathematics.
Tasks :
1) Compare general concepts in mathematics and dance.
2) Analyze results.
3) Prove received connection in practice.
Object research: mathematics and dance
Stages of work:
I stage - preparatory
1. Selection literature on the topic
2. Study theoretical basis for establishing a connection between mathematics and dance
3.Definition goals and objectives.
4. Selection material for the development and conduct of research.
II stage - pr a static
1.Research dance and mathematics through the study of literature
2. Research mathematics in dance by observing in the process of dancing
III stage - generalizing
1. Generalization and analysis of results practical stage.
2. Conclusions.
Methods studies we used: theoretical and empirical
1. Observation.
2. Analysis
3. Systematization
4. Summary
Chapter 1. Geometry in the dance
1.1 Wantle 9000 9000
P. at first glance, this is the step that could be skipped, but the warm-up before training, warms up the muscles and ligaments, so that they become more plastic, which, in due time, makes it possible to avoid unwanted injuries and sprains that abound in dance training. Didn't put it right foot, stumbled, slipped - and as a result of sprain.
Each warm-up should include: tilts and rotation of the head, exercises for shoulders, dilution and reduction of the shoulder blades, light stretching and tilting of the body, stretching the hips (light) and moving the pelvis. The main thing is to reproduce implementation is correct.
Follow start from the head. Turning the head clockwise and counterclockwise a certain circle appears, and, tilting the head in opposite directions, 2 lines perpendicular to each other are formed. Stretching the shoulders and elbow joint, we also form a circle. Legs should also not be left without attention. So, rotating the knees, we knead the knee joint, forming another circle.
1.2 Stretch
Almost each dancer has a stretch after the warm-up, which continues to leave muscles are toned. At this point, you should also correctly perform the movements, which are also related to mathematics. So where to raise 1 leg, it is necessary to form a right angle, since it is in this position that the muscles stretched.
Most the following exercise is popular, but, unfortunately, many people do it not properly. Spreading your legs to the sides, you need to form an obtuse angle, ideally 180 degrees, the same must be done with the hands. For the line of legs we will take the AB line, behind the hand line - the CD line, and behind the body line - the MH line. As a result of this exercise, AB//CD is formed at the secant MH. It is with such muscle structures will stretch.
1.3 Drawing
After of the previous points, the dancer proceeds to the dance itself. When placing a drawing concepts such as symmetry and asymmetry are used
Without geometric shapes according to the famous choreographer Zakharov R. V., no dance either among the people or on the stage: circles, ellipses, parallel lines, diagonals, squares, triangles, spirals - we use all this in a dance pattern.
• Zakharov R. V. offers us his classification of types of dance pattern:
1.
3.1 Diagonal
Diagonal used in dances very often, both in folk and classical. By diagonal is very beneficial to perform all kinds of movements that require rapid dynamics, - air flights, running on the fingers, various rotations etc. - it all depends on the idea, on the construction of the combination, the style of the character dance.
1.3.2 Circle
Circle dances - the movement of dancers in a circle - originate in ancient times. In the time of paganism dances were led in a circle, depicting the circular movement of the sun. It is still the most common figure in almost all folk dances: Russian round dances, Ukrainian hopaks, Belarusian, Moldavian, dances of peoples Caucasus, Eastern and Western Europe and others are built on a circle drawing.
1.3.3 Symmetry
“Symmetry” - a word that came into our language from the ancient Greeks, who first turned to it the phenomenon of attentive attention and those who tried to study it.
The term means the presence of a certain system, as well as a harmonious combination of parts of the object. C since ancient times, symmetry is an essential concept for the development of mankind in various fields and industries. That is why this term has become an integral part of the dance. It is tracked down in many early ballets, where the dancers in the same number lined up in lines and created a homogeneous scene on the stage construction. Symmetry is inherent in a lot the number of ballet fundamental decisions. So, the first one is symmetrical. second and sixth leg position. There are several types of symmetry in dance.
1.3.4 Asymmetry
Pushing off from the thought of symmetry, the creative society came to the creation of innovative and valuable works of art in different areas of dance. Many contemporary works based on the principle of asymmetry, which evolves from the natural asymmetry of movement into complex settings.
Location of dancers on stage the spatial organization of the positions of their bodies and body parts today is often asymmetrical. We are currently witnessing a developed aesthetic harmony between the principles of symmetry and asymmetry embodied on the stage. Asymmetry has interesting possibilities that symmetry does not have. She is unpredictable, strange, unusual. She reveals the secret of movement in a greater degrees than symmetry.
1.3.5 Communication symmetry and asymmetry
No it cannot be assumed that an excess of asymmetry will make the dance more interesting. Necessary balance between asymmetry and symmetry, excluding the leveling of art and everyday life. We encounter asymmetry not only on the stage, but also constantly in everyday life. Symmetry is more rare. Thus, a pledge creating a successful staging is the harmony between the two principles. Yes, on in this picture, the figure acts as a symmetry, and the figure acts as an asymmetry position of the main characters.
1.4 Figures
Any it is possible to mentally bring a dance figure into an n-gon. Geometric the figure is stable if the center of gravity is correctly calculated. So Thus, stability is of particular importance for dance.
On balance is greatly influenced by the projection of the overall center of gravity. The closer to support the center of gravity of the body and the larger its area, the higher the resistance of the body. Generally all figures in the dance can be divided into stable and unstable. To sustainable dance figures include a square, a rectangle, a triangle with the larger side at the base, a trapezoid with a large lower base and a rhombus.
K unstable figures include a triangle with a smaller side at the base, a triangle based on a vertex, a parallelogram, a circle.
Unsteady the poses are characterized by instantaneous execution of the element, acrobatic character. The dancer takes them at a high musical intensity.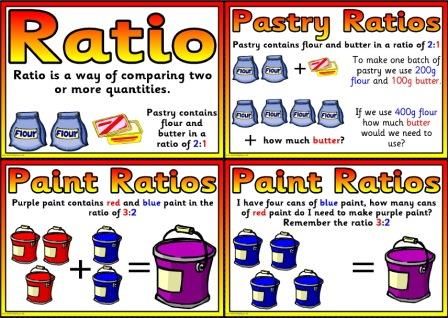
To the unstable elements, except for poses, include jumps, runs, turns.
Chapter 2. Algebra in dance
2.1 Functions
Create a beautiful dance is impossible without graphs of mathematical functions. Function Graph - a concept in mathematics that gives an idea of \u200b\u200ba geometric image functions. There are various types of function graphs and their representation in the dance, let's give some examples.
1) With such a movement as a diagonal, a linear function y=x is formed.
Himself the graph is a bisector for I and III coordinate quarters.
2) If in classical dance, take the third position of the hands, you get a parabola, and the function will be quadratic.
3) If you take a preparatory position in a classical dance, you get a parabola whose branches are directed downwards, and the function will be quadratic.
4) If in classical dance, leave the left hand in a preparatory position, and the right in third position, then the graph will be a cubic parabola, and the function will be cubic.
5)B modern style dances, one of the most popular are hand waves, in resulting in a sinusoid graph, and its function is trigonometric function.
2.2 stroke
stroke– an essential concept, in the absence of which it is difficult to disassemble the dance into components parts. In order to calculate the music, you need to hear it. Easiest do this by listening to percussion instruments. There are also the most accurate methods break the music into squares (4 counts) and eights.
B in any dance, the beat is significant, but We learn to count only with the help of arithmetic. Right here for you math will also be needed, correct counting will improve your understanding dance, and you will stop straying if you are aware of the dance count.
K For example, if we talk about cha-cha-cha, then when evaluating here, such characteristics, such as the position of the foot on the blow at the expense of 1,2,3,4, also, time, required to complete a step, measured in fractions of a second, etc.
2.3 Planet Dance
B modern world are able to make beautiful movements not only people, but also celestial bodies. The planets in the sky move in graceful orbital models, dancing to the Music of the Cosmos. There is more mathematical and geometrical harmony in these movements, than we think.
Take orbits of any two planets, and draw a line between the two positions of the planet for every few days. Because a planet moving in an inner orbit moves faster than the one moving along the outer orbit, then interesting models. Each planetary couple has its own unique dance rhythm. For example, the dance of Earth and Venus returns to its original position after eight earth years.
Eight Earth years equals thirteen years of Venus.
Earth: 8 years * 365.256 days per year = 2922.05 days
Venus: 13 years * 224.701 days in a year = 2921.11 days (i.e. 99.9%)
(On the video shows the dance of Venus and Earth)
Chapter 3. Practice
3.1 Task
Teacher dances, it is necessary to put on the dance "Casket", where 9 girls participate. They are stand in a column in the middle of the central wall. On beats 1-7, the last girl, making a semicircle, becomes the beginning of the column. On bars 8-15, the rest, following leading, are rebuilt in a large circle. The lead girl is slowly spinning in the center of the circle. When the music ends, they all turn to face in a circle and raise up the joined hands, forming a polygon. How many bars it will take the leader to approach all the joined hands and go back, given that for each trip from the center of the circle to the arms, 2 strokes? Find the total number of measures in the dance.
conclusion contains figures, fractions, proportions. Another fact confirming the connection between dance and mathematics is the use of general terms: lines, diagonals, in the figure dances can be arranged symmetrically or asymmetrically.
U dancer, there is always a sense of balance, center, that is, the dancer is in the coordinate system. Behind the dance plasticity you can see not only the creation of poses, geometric shapes, drawing, but also the exact mathematical movement calculation.
Also It has been proven that dancing actively influences the human brain activity, for confirmation of my words, I will turn to the research of scientists. Their results show that for the development of mental activity it is necessary to combine mathematics and dances, i.e., body movements must coincide with mathematical concepts, and this information is processed by the brain.
Repeatedly proven that professional dancers in old age almost never face senile sclerosis.
This aspect is due to the fact that regular visits dancing contributes to the maintenance of neural connections that are involved in forming sustainable habits and filtering important incoming information from one that doesn't really matter.
Americans have repeatedly published studies that have proven the positive impact dancing on brain activity. In the process of movement to the music occurs activation of several areas of the brain that count spatial analysis, emotions and the power of movements.
Also during dances, the main channels of information perception are involved, in in particular visual, kinetic, auditory, visual, auditory and tactile. Naturally, such a load on the brain improves its activity, contributes to the development and strengthening of memory, rapid reaction to external change, spatial thinking. In addition, dance classes teach really feel the music. This helps develop a sense of rhythm and artistic taste.
Our the goal is that there is an inextricable link between mathematics and dance, confirmed.
B In conclusion, I would like to add that the part of the youth that have not yet chosen what sport to do, I suggest paying attention to dancing. This is a healthy lifestyle, and beauty, and an accurate mathematical calculation.
9000
068
References
1.Zinaida Root "Dancing with notes" 2006 Moscow "Iris Press"
2. http://xn--80aexocohdp.xn--p1ai/20-%D0%B8%D0%BD%D1%82%D0%B5%D1%80%D0%B5%D1%81%D0%BD%D1 %8B%D1%85-%D1%84%D0%B0%D0%BA%D1%82%D0%BE%D0%B2-%D0%BE-%D1%82%D0%B0%D0%BD% D1%86%D0%B0%D1%85/
3. https://a-dance.ru/articles/etiket-v-tantsah/
4. https://masterok.livejournal.com/4011657.html
5. https://ru.wikipedia.org/ wiki/%D0%A1%D0%BB%D0%BE%D0%B2%D0%B0%D1%80%D1%8C_%D1%82%D0%B5%D1%80%D0%BC%D0%B8 %D0%BD%D0%BE%D0%B2_%D0%B1%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85_%D1%82%D0%B0%D0 %BD%D1%86%D0%B5%D0%B2
6.
https://academy-expert.com/psikhologiya/pro-osnovnyye-figury-v-tantse
7. https://ru.wikipedia.org/wiki/%D0%A2%D0 %B0%D0%BD%D0%B5%D1%8
8. Alex Moore "European Dance Technique Revisited" 1993
St. Petersburg
9. Walter Laird "Technique of Latin American dances" 2003 "Artis" Moscow
10. http://wdoxnovenie.ru/stati/2365/dvizhenija-dlja-tanca/
Mathematics in dance
- Authors
- Executives
- Job files
- Award documents
Gedygusheva A.M. 1
1GBOU of Moscow "School No. 354 named after D.M. Karbyshev"
Postavnichiy Yu.S. 1
1GBOU of Moscow "School No. 354 named after D.M. Karbyshev"
The author of the work was awarded a diploma of the winner of the II degree
Diploma of a school student Certificate of the head
The text of the work is placed without images and formulas.
The full version of the work is available in the "Files of the work" tab in PDF format
Introduction
Science and art are two main principles in culture, two complementary forms of human creative activity.
From birth, we are surrounded by the world of precise calculations. The original meaning of the word "mathematics" (from the Greek mathema - knowledge, science, in particular, in Latin ars mathematica, means the art of mathematics) has not been lost even today, it remains a symbol of wisdom, the queen of all sciences. The beauty of mathematics among the sciences is very great, and beauty is one of the links between science and art. Of the many arts with which mathematics interacts, I decided to choose choreography.
Dance has been present in human life since ancient times. Among primitive people, love, work and ritual are embodied in dance movements. Each of us at least once danced or watched the performance of the dance.
Just think how much mathematics is in the dance!
Dance contains figures, fractions, proportions. Another fact that confirms the connection between dance and mathematics is the use of common terms: lines, diagonals, in a dance pattern can be parallel or perpendicular, symmetrical or asymmetrical. The paper presents graphical implementations of the sections described in the paper.
In addition to visible geometric figures and algebraic forms, the dancer always has a sense of balance, center, that is, the dancer is in the coordinate system.
Behind the dance plasticity one can see not only the creation of poses, geometric figures, drawings, but also the exact mathematical calculation of the strength of the jump, the number of turns in the round, the length and width of the step. Many dance moves are easier to perform if you know their math.
Dance is both a healthy lifestyle, and beauty, and an accurate mathematical calculation.
Problem: Knowing math makes it easier to learn dance.
Relevance: my many years of experience in choreography shows that dance has much in common with such a science as mathematics, since rhythm, tempo, dance figures obey certain mathematical laws and concepts.
Mathematics is inextricably linked with everyday life, in which there is a place for dancing. Mathematical tasks develop thinking, logic, a set of analytical skills: the ability to group objects, reveal patterns, determine relationships between phenomena, and make decisions.
Dancing has a beneficial effect not only on the physical form, but also on mental abilities, spatial imagination. A reasonable combination of dancing and mathematics allows you to develop mental abilities.
Purpose of work: to identify points of contact between mathematics and choreography on the example of studying dances based on the construction of geometric figures and dance movements from the point of view of mathematical accuracy
Tasks:
1.
study dance movements and associate them with mathematical concepts;
2. analyze the connection between dance and mathematics;
3. to consider the application of acquired knowledge in choreography.
Research object: Choreographic movements.
Subject of study: Mathematical description of choreographic movement.
Hypothesis: dance and mathematics are closely related.
Research methods:
1. Working with educational and popular science literature, Internet resources;
2. Observation, comparison, analogy;
3. Analysis of own practical experience.
1. Basic concepts
Dance – a type of art in which an artistic image is created through rhythmic plastic movements and a change in the expressive positions of the human body.
Algorithm
In everyday life, each person is faced with the need to solve problems of varying complexity. Some of them are difficult and require long reflections to find solutions, while others, on the contrary, are so simple and familiar that they are solved automatically. At the same time, the execution of even the simplest task is carried out in several successive stages (steps). In the form of a sequence of steps, it is possible to describe the process of solving many problems known from the school mathematics course. Since mathematical science is associated with the concept of an algorithm (“step by step”) and sequence, and a dance step is both a sequence and an order of movements, it follows that dance and mathematics are connected by the general concept of “step”.
Algorithms are used to perform similar tasks to speed up the process of achieving results. The essence of the algorithm is that, having learned to perform elementary operations, in the future we do not think about the order in which they are performed.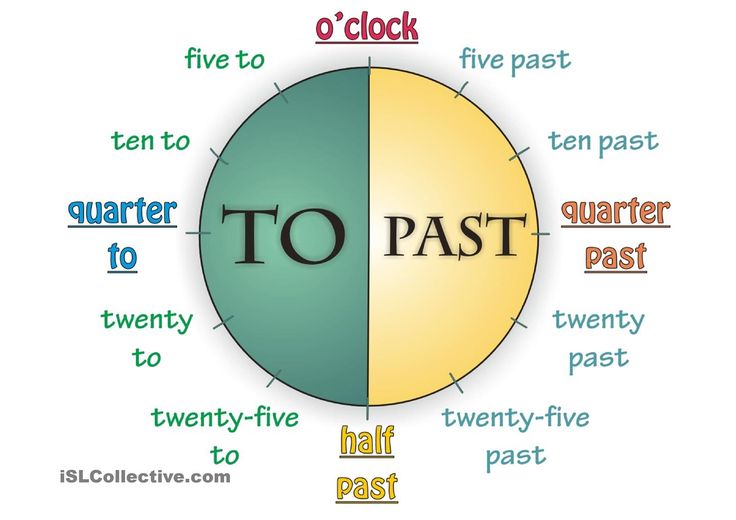
As in mathematics, dance has its own set of aspects that must be mastered in the early years of training in order to bring them to automatism.
Dance can be considered not only as a sequence of interrelated movements, but also as an algorithm.
American choreographer William Forsyth created a dance technique he called "Dance Geometry" or "Technology of Improvisation". Using this technique, the dancer draws imaginary geometric shapes in the air and then drags their limbs through this complex and invisible geometry. It turned out a new interesting direction in modern dance.
In the modern world, a dance has appeared, called "Technology of Improvisation". Using this technique, the dancer draws imaginary figures in the air and then drags their limbs through this complex and invisible geometry.
To make this geometry visible, a computer animation superimposed on a motion video is used.
First, the dancers imagine lines in space that could curve, ripple, or deform in other ways.
Moving from a point to a line, then to a plane, then to a volume, they visualize a geometric space made up of individual points with a huge number of interconnections. Since these points are inside the dancer's body, no relative movement is required.
2. Relationship between dance and mathematics
2.1 Function curves
It is impossible to create a beautiful dance without graphs of mathematical functions. A beautiful dance is a beautiful schedule. In each dance movement, you can find a graph of one of the mathematical functions.
Often, when dancers spread their arms or even legs in different directions, it turns out - a straight line. And when they stand in a circle, it turns out a circle.
If you stand in attitude, this is one of the basic postures in classical dance, in which the balance is maintained on one leg, and the other leg is raised and laid back in a bent position, you get a broken line.
If you take the third open position of the hands in a classical dance, you get a parabola. If we cross pairs of partners' hands and make wave movements, we will involuntarily get the sign of infinity.
2.2. Geometric shapes
Angle is a geometric figure that consists of a point and two rays emanating from this point. These rays are called the sides of the angle, and their common origin is called the vertex of the angle. The unit of measure for angles is degrees. In mathematics, the following types of angles on a plane are distinguished depending on the degree measure of the angle: acute, straight, obtuse and developed.
Vertical twine
Dancers during the performance take various poses, alternating with other elements of the dance. A posture in dance is understood as a stop in motion, in which the dancer's body is in a stationary position of balance.
In the choreography it's called " dot ".
Also, the concept of "point" is used when performing any turn or rotation when it is important to maintain balance. This is obtained precisely due to the ability to focus the gaze or “keep the point”.
Point - body position. In order for a continuous and sometimes quite fast movement to be learned at a slow pace, the dance is considered as a series of postures connected by intermediate movements, each of which is called a point. If a stop occurs at one of the points, it is called a fixed point. If there is no stop or it is taken conditionally in order to understand through what intermediate stages the movement from one fixed point to another occurs, we speak of the presence of a passing point, that is, the position of the body in which we do not linger.
An important mathematical concept is straight line . In ballet schools, dancers are taught to work with lines in space, since every dance pattern is made up of lines (straight lines).
During the dance, when one pattern replaces another, the dancer must "keep the line", that is, adhere to the trajectory along which the rebuilding occurs. One of the main criteria for evaluating a dance is beautifully and correctly lined lines.
In hand positions
(3rd position)
In mathematics, two separate concepts are distinguished: circle and circle . In choreography, the circle is predominantly seen in the dance pattern. In their own work, choreographers and choreographers often use a different name - a circle.
On the move
The most ancient form of Russian folk dances is round dance, which forms a circular structure. Often you can find a double circle (a circle within a circle). Sometimes the dancers form two circles side by side, and sometimes these circles seem to overflow one into the other and their movement forms a figure-eight pattern. Large and small circles are a very common form of building a Russian round dance.
2.3. Symmetry and asymmetry
In mathematics, there are several types of symmetry: axial (relative to a straight line), central (relative to a point), mirror (relative to a plane). Symmetry in dance is a harmonious, easy-to-observe element of choreography that is necessary to create the basic structure of the dance. There are also several types of symmetry in the dance: the symmetry of the ballet positions of the legs, arms, body, head; symmetry of the dance pattern; symmetry of the movements performed.
Symmetry in dance is a calm, unruffled, logical and simple element of choreography. The principle of symmetry can be traced in many early ballets, where dancers lined up in equal numbers and formed a homogeneous structure on the stage, having a center and (or) axis of symmetry. Symmetry is also called the situation in which all dancers perform the same movement at the same time. Symmetry is the balanced arrangement of the dancer's body, the location of the dancer's body in space.
For example, a ballerina ends her number with a sparkling fouette when she spins on one leg a certain number of times.
It is the repetition of these movements (the stem repeatedly describes a circle that has many axes of symmetry - diameters and a center of symmetry) that determines their aesthetic effect.
Matilda Kshesinskaya became the first Russian ballerina to perform 32 fouettes at the Mariinsky Theatre.
Symmetry of ballet positions of legs, arms, body, head
Dance Symmetry
(formation of a homogeneous structure on the stage in lines and drawings)
However, to produce the proper effect, symmetry must be accompanied by asymmetry.
Asymmetry is an unexpected and unusual element, and therefore makes the dance more interesting for the observer. It reveals the movements to a greater extent, makes the dance alive, saturating it with unpredictable elements.
This principle is more often used than symmetry.
Thus, using the principles of symmetry and asymmetry, the choreographer achieves the exact expression of his idea. The key to creating a successful production is the harmony between the two principles.
2.4. Parallelism and perpendicularity
As in mathematics, in dancing it is necessary to observe a clear construction of figures. In order for the viewer to see beautiful choreography on stage, parallelism is used: parallel positions, parallel to a partner, parallel to the floor.
When dancers perform the same elements of the dance, synchronization must be observed. The coordination of movements of one partner to another is characterized by the parallelism of each part of the body of one dancer to another. This principle in dance is called the "Principle of Parallel Partners".
Also in the dance there are certain standards for the correct execution of movements.
One of the standards is the parallelism of body parts to the floor when performing a dance element. So, for example, a grand jet is a jump in which both legs of the dancer must be parallel to the floor, etc.
Perpendicularity is used in the same way. Perpendicular to the floor - an element of dance in which any part of the body is perpendicular to the floor. Perpendicularity of body parts - an element of dance in which body parts are perpendicular to each other (for example, grand batman).
2.5. Turn
Turn - this term means a turn around its axis by 360 ° (one turn), half a turn - a turn by 180 °, a quarter - by 90 °, two turns - 720 °, etc.
Fuete is a series of consecutive rotations in place, during which the leg opens 45 ° with each rotation.
Tour - rotation of the body around the vertical axis by 360°. Pirouette is a 360° turn on one leg.
Each dance figure can be mentally inscribed in an n-gon. A geometric figure is stable if the center of gravity is correctly calculated. The center of gravity is the point through which the line of action of the resultant elementary forces of gravity passes. Stable figures: a triangle with a larger side at the base, a trapezoid with a large base at the bottom, a square, a rectangle.
Conclusion.
In my work I compared dance with mathematics. Based on the foregoing, we can conclude that the dance pattern contains geometric shapes, lines, diagonals, circles. Dancers move along their trajectories, subordinating their movements to the musical rhythm and tempo. They can be parallel or perpendicular, symmetrical or asymmetrical. Moreover, the position of the body in the dance is fixed by various angles - sharp, obtuse, straight.
In addition to visible geometric shapes and algebraic forms, the dancer always has a sense of balance, center, that is, the dancer is always in the coordinate system.
Behind the dance plastique we can see not only the creation of poses, geometric figures, drawing, but also the calculation of the strength of the jump, the number of turns in the round, the length and width of the step, the acceleration and deceleration of movement. Thus, mathematical logic is manifested in the dance, the laws of algebra and geometry are used.
Therefore, using the algorithm for teaching classical dances, basic mathematical concepts and principles, the choreographer achieves an accurate expression of his idea, which is the key to creating a beautiful and successful dance production.
Linking the elements of the dance, we build logical chains. Spatial imagination develops.
Dancing is a good way to train your intellect! Schoolchildren who have completed a one-year dance course do better on tests in geometry and mathematics than those who have never danced (Harvard University, USA).
Professional dancers perform better on attention tests (Studies in Canada).
So, the mathematical component of the dance is contained in the pattern of the dance, in the movements of the dancer, in the classical positions. Dance is both a healthy lifestyle, and beauty, and an accurate mathematical calculation.
Literature:
Basics of classical dance. Edition 6. Series “Textbooks for universities. Special literature "- St. Petersburg: Publishing house" Lan ", 2000.
Okuneva. M. Russian folk round dances and dances: a methodological collection for working with children: APN RSFSR, 1948.
Pisarev, A. Classical dance school 1976; Publishing house: L.: Art
Purtova T.V., Belikova A.N., Kvetnaya O.V. / Teach children to dance: a tutorial. Moscow: Vlados. 2003.
Smirnov, I.
